Rangkuman
Praktikum Sistem Digital Modul 1-6
Disusun
Oleh :
Nama
: Azizah Sophia Azzahra
NIM
: 221080200151
Kelompok
: 9
Assalamu'alaikum
Wr. Wb.
Materi yang saya lampirkan merupakan hasil rangkuman dari materi Praktikum Sistem Digital satu semester ini dan menjadi salah satu syarat untuk memenuhi tugas Praktikum Sistem Digital. Saya merupakan Mahasiswi Universitas Muhammadiyah Sidoarjo dari Program Studi Informatika. Jika ingin lebih tahu tentang Universitas Muhammadiyah Sidoarjo bisa langsung mengakses link umsida.ac.id atau fst.umsida.ac.id
POKOK
BAHASAN I
PENGENALAN GERBANG LOGIKA DASAR
TUJUAN
Setelah menyelesaikan percobaan ini, mahasiswa diharapkan mampu :
- Memahami pengoperasian gerbang logika dasar
- Merancang dasar-dasar rangkaian logika
- Menjalankan modul rangkaian logika
- Menerapkan gerbang-gerbang dasar dalam bentuk Rangkaian terintegrasi
PEMBAHASAN
Tampilan Digital Works
Dalam lembar kerja diatas terdapat 6 point penting toolbar yang akan dijelaskan dalam gambar berikut.
1. Gerbang AND
Gerbang AND memerlukan 2 atau lebih. Masukan (Input) untuk menghasilkan hanya 1 Keluaran (Output). Gerbang AND akan menghasilkan Keluaran (Output) Logika 1 jika semua masukan (Input) bernilai Logika 1 dan akan menghasilkan Keluaran (Output) Logika 0 jika salah satu dari masukan (Input) bernilai Logika 0. Rangkaian AND dinyatakan sebagai Z = A*B atau Z = AB (tanpa symbol).
Simbol Gerbang AND
2. Gerbang OR
Gerbang OR memerlukan 2 atau lebih Masukan Input) untuk menghasilkan hanya 1 Keluaran (Output). Gerbang OR akan menghasilkan Keluaran (Output) 1 jika salah satu dari Masukan (Input) bernilai Logika 1 dan jika ingin menghasilkan Keluaran (Output) Logika 0, maka semua masukan (Input) harus bernilai Logika sebagai Z = A + B.
Simbol Gerbang OR
3. Gerbang NOT
Gerbang NOT hanya memerlukan sebuah. Masukan (Input) untuk menghasilkan hanya 1 Keluaran (Output). Gerbang NOT disebut juga dengan Inverter (Pembalik) karena menghasilkan Keluaran (Output) yang berlawanan (kebalikan) dengan Masukan atau Inputnya. Berarti jika kita ingin mendapatkan Keluaran (Output) dengan nilai Logika 0 maka Input atau Masukannya hams bernilai Logika 1. Rangkaian NOT dinyatakan sebagai Z = A’.
Simbol Gerbang NOT
4. Gerbang NAND (NOT AND)
Arti NAND adalah NOT AND atau BUKAN AND, Gerbang NAND merupakan kombinasi dari Gerbang AND dan Gerbang NOT yang menghasilkan kebalikan dari Keluaran (Output) Gerbang AND. Gerbang NAND akan menghasilkan Keluaran Logika 0 apabila semua Masukan (Input) pada Logika 1 dan jika terdapat sebuah Input yang bernilai Logika 0 maka akan menghasilkan Keluaran (Output) Logika 1. Rangkaian NAND dinyatakan sebagai Z = (A * B)’.
Simbol Gerbang NAND
5. Gerbang NOR (NOT OR)
Arti NOR adalah NOT OR atau BUKAN OR, Gerbang NOR merupakan kombinasi dari Gerbang OR dan Gerbang NOT yang menghasilkan kebalikan dari Keluaran (Output) Gerbang OR. Gerbang NOR akan menghasilkan Keluaran Logika 0 jika salah satu dari Masukan (Input) bernilai Logika 1 dan jika ingin mendapatkan Keluaran Logika 1, maka Semua Masukan (Input) hams bernilai Logika 0. Rangkaian NOR dinyatakan sebagai Z = (A+B)’.
Simbol Gerbang NOR
6. Gerbang X-OR (Exclusive OR)
X-OR adalah singkatan dari Exclusive OR yang terdiri dari 2 Masukan(Input) dan 1 Keluaran (Output) Logika. Gerbang X-OR akan menghasilkan Keluaran (Output) Logika 1 jika semua Masukan - masukannya (Input) mempunyai nilai Logika yang berbeda. Jika nilai Logika Inputnya sama, maka akan memberikan hasil Keluaran Logika 0. Rangkaian X-OR dinyatakan sebagai Z = (A’*B) + (A*B’) = A+B.
Simbol Gerbang X-OR
7. Gerbang X-NOR (Exclusive NOR)
Seperti Gerbang X-OR, Gerbang X-NOR juga terdiri dari 2 Masukan (Input) dan 1 Keluaran (Output). X-NOR adalah singkatan dari Exclusive NOR dan merupakan kombinasi dari Gerbang X-OR dan Gerbang NOT. Gerbang X-NOR akan menghasilkan Keluaran (Output) Logika 1 jika semua Masukan atau Inputnya bernilai Logika yang sama dan akan menghasilkan Keluaran (Output) Logika 0 jika semua Masukan atau Inputnya bernilai Logika yang berbeda. Hal ini merupakan kebalikan dari Gerbang X-OR (Exclusive OR). Rangkaian X-NOR dinyatakan sebagai Z = (A+B)' = A*B.
Simbol Gerbang X-NOR
POKOK
BAHASAN II
PERSAMAAN
BOOLEAN & PENYEDERHANAAN RANGKAIAN LOGIKA (MENGGUNAKAN METODE K-MAP)
TUJUAN
Setelah menyelesaikan percobaan ini Mahasiswa diharapkan mampu :
- Membuat sebuah rangkaian logika sederhana melalui persamaan Boolean dan label kebenaran yang diketahui.
- Menggunakan K-map untuk memecahkan persoalan desain rangkaian logika sederhana.
DASAR TEORI
A. Aljabar Boolean
Aljabar Boolean memuat variable dan simbol operasi untuk gerbang logika. Simbol yang digunakan pada aljabar Boolean adalah: (.) untuk AND, (+) untuk OR, dan ( ) untuk NOT. Rangkaian logika merupakan gabungan beberapa gerbang, untuk mempermudah penyeleseian perhitungan secara aljabar dan pengisian tabel kebenaran digunakan sifat-sifat aljabar Boolean.
Dalam aljabar boolean digunakan 2 konstanta yaitu logika 0 dan logika 1. Etika logika tersebut diimplementasikan kedalam rangkaian logika maka logika tersebut akan bertaraf sebuah tegangan. Kalau logika 0 bertaraf tegangan rendah (aktive low) sedangkan kalau logika 1 bertaraf tegangan tinggi (aktive high). Pada teori-teori aljabar boolean ini berdasarkan aturan-aturan dasar hubungan antara variable-variabel Boolean.
Dalil-dalil Boolean (Boolean postulates)
- Pl: X = 0 atau X = 1
- P2: 0 . 0 = 0
- P3: 1 + 1 = 1
- P4: 0 + 0 = 0
- P5: 1 . 1 = 1
- P6: 1 . 0 = 0 . 1 = 0
- P7: 1 + 0 = 0 + 1 = 1
Theorema Aljabar Boolean
- T1: Commutative Law
a. A + B = B + A
b. A . B = B . A
- T2: Associative Law
a. (A+B)+C=A+(B+C)
b. (A.B).C=A.(B.C)
- T3: Distributive Law
a. A.(B+C)=A.B+A.0
b. A+(B.C)=(A+B).(A+C)
- T4: Identity Law
a. A+A=A
b. A . A = A
- T5: Negation Law
a. ( A' )=A'
b. ( A' )' = A
- T6: Redundant Law
a. A+A.B=A
b. A.(A+B)=A
- T7: 0+A=A
a. 1 . A = A
b. 1 + A = 1
c. 0 . A = 0
- T8: A' + A = 1
a. A'. A = 0
- T9: A + A ' . B = A + B A . (A' + B) = A . B
- T10: De Morgan's Theorem
a. (A+B)' = A'.B'
b. (A.B)' = A'+B'
B. K-Map
Peta Karnaugh (Karnaugh Map, K-map) dapat digunakan untuk menyederhanakan persamaan logika yang menggunakan paling banyak enam variable. Dalam laporan ini hanya akan dibahas penyederhanaan persamaan logika hingga empat variable. Penggunaan persamaan logika dengan lima atau enam variable disarankan menggunakan program computer.
Peta merupakan gambar suatu daerah. Peta karnaugh menggambarkan daerah logika yang telah di jabarkan pada table kebenaran. Penggambaran daerah pada peta karnaugh hams mencakup semuah logika. Daerah pada Peta Karnaugh dapat tamping tindih antara satu kombinasi variable dengan kombinasi variable yang lain.
PEMBAHASAN
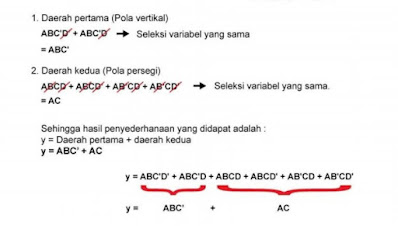
1. K-Map 2 Variabel
Pada K-Map 2 variabel, variabel yang digunakan yaitu,
Misalnya variabel A & B.
Catatan :
- Untuk setiap variabel yang memiliki aksen, maka di dalam tabel ditulis 0.
- Untuk setiap variabel yang tidak memiliki aksen, maka di dalam tabel ditulis 1.
Contoh : A' (ditulis 0), B (ditulis 1)
Desain/model pemetaan K-Map 2 variabel dapat dibentuk dengan 2 cara seperti pada Gambar dibawah ini. Pada pembahasan ini, penulis menggunakan desain pemetaan Model 2 seperti berikut :
Dalam menentukan hasil penentuan, ambil daerah yang berbentuk seperti berikut
2. K-Map 3 Variabel
3. K-Map 4 Variabel
Pada K-Map 4 variabel, variabel yang digunakan. Misalnya variabel A, B, C & D. Desain pemetaan K-Map 4 variabel dapat dibentuk dengan 2 cara seperti pada Gambar dibawah ini. Pada pembahasan ini, penulis hanya menggunakan desain pemetaan Model 2 seperti berikut :
POKOK
BAHASAN III
MULTILEVEL NAND DAN NOR
TUJUAN
Setelah menyelesaikan percobaan ini Mahasiswa diharapkan mampu :
- Mengerti cara meng-implementasikan teorema de Morgan ke bentuk NAND dan NOR
- Membuat rangkaian pengganti AND, OR, NOT ke NAND dan NOR dengan persamaan de Morgan
- Merubah rangkaian AND, OR, NOT menjadi NAND atau NOR saja secara langsung
DASAR TEORI
Gerbang NAND dan NOR merupakan gerbang universal, artinya hanya dengan menggunakan jenis gerbang NAND saja atau NOR saja dapat menggantikan fungsi dari 3 gerbang dasar yang lain (AND, OR, NOT). Multilevel, artinya : dengan mengimplementasikan gerbang NAND atau NOR, akan ada banyak level / tingkatan mulai dari sisi input sampai ke sisi output. Keuntungan pemakaian NAND saja atau NOR saja dalam sebuah rangkaian digital adalah dapat mengoptimalkan pemakaian seluruh gerbang yang terdapat dalam sebuah IC logika sehingga kita bisa lebih mengirit biaya dan juga irit tempat karena tidak terlalu banyak IC yang digunakan (padahal tidak semua gerbang yang ada dalam IC tersebut yang digunakan).
Adapun cara melakukan konversinya dapat kita lakukan dengan dua cara yaitu:
1. Melalui peneyelesaian persamaan logika/Boolean
2. Langsung menggunakan gambar padanan
PEMBAHASAN
1. NAND
Kalau persamaan awal (soal) kita buatkan rangkaian digitalnya, maka akan terlihat rangkaian seperti berikut:
Pada gambar di atas dapat kita lihat bahwa rangkaian terdiri dari sate buah gerbang NOT, dua buah gerbang AND dan dua buah gerbang OR. lni artinya kita hares membeli tiga macam IC yaitu AND, OR dan NOT, tetapi tidak semua gerbang yang ada dalam IC tersebut terpakai dalam rangkaian. Artinya adalah kita sudah melakukan pemubaziran (membuang sia-sia) gerbang lainnya, padahal kita sudah beli dan banyak memakan tempat.
Setelah penyederhanaan dengan menggunakan persamaan logika di atas kita dapat membuat rangkaian logika baru dengan gerbang NAND saja yang kalau kita gambarkan rangkaiannya seperti berikut:
Dengan cara di atas terlihat kita hanya menggunakan dua IC NAND untuk mebangun sebuah rangkaian yang berfungsi sama. Ini berarti kita sudah bisa menghemat uang dan tempat.
2. NOR
Selesaikanlah persamaan tersebut dengan menggunakan gerbang NOR saja.
Jawab:
Sedangkan rangkaian setelah diubah ke bentuk NOR saja adalah sebagai berikut:
Dari gambar terlihat bahwa dengan membuat rangkaian menjadi berbentuk NOR saja kita tetap hanya membutuhkan dua buah IC saja yang terpakai semuanya (tidak mubazir atau terbuang).
POKOK BAHASAN IV
RANGKAIAN ARITMATIKA DIGITAL
TUJUAN
Setelah menyelesaikan percobaan ini Mahasiswa diharapkan mampu :
- Memahami cara kerja rangkaian half adder dan full adder serta half subtractor dan Buol subtractor.
- Membuat rangkaian half adder dan full adder serta half subtractor dan Buol subtractor dari rangkaian kombinasi gerbang logika dasar.
- Memahami perbedaan Carry in dengan Carry out terhadap Full Adder serta pengaruh yang di timbulkannya
PEMBAHASAN
1. Adder
Rangkaian Adder (penjumlah) adalah rangkaian elektronika digital yang digunakan untuk menjumlahkan dua buah angka (dalam sistem bilangan biner), sementara itu di dalam computer rangkaian adder terdapat pada mikroskoper dalam blok ALU (Arithmetic Logic Unit). Sistem bilangan yang digunakan dalam rangkaian adder adalah :
- Sistem bilangan Biner (memiliki base/radix 2)
- Sistem bilangan Oktal (memiliki base/radix 8)
- Sistem bilangan Desimal (memiliki base/radix 10)
- Sistem bilangan Hexadesimal (memiliki base/radix 16)
Namun, diantara ketiga system tersebut yang paling mendasar adalah system bilangan biner, sementara itu untuk menerapkan nilai negatif, maka digunakanlah system bilangan complement. BCD (binary-coded decimal).
a. Half Adder
Half adder adalah suatu rangkaian penjumlah sistem bilangan biner yang paling sederhana. Rangkaian ini hanya dapat digunakan untuk operasi penjumlahan data bilangan biner sampai 1 bit saja. Rangkaian half adder mempunyai 2 masukan dan 2 keluaran yaitu Sunmamary out (Sum) dan Carry out (Carry).
Rangkaian ini merupakan gabungan rangkaian antara 2 gerbang logika dasar yaitu X-OR dan AND. Rangkaian half adder merupakan dasar bilangan biner yang masing-masing hanya terdiri dari satu bit, oleh karena itu dinamakan penjumlah tak lengkap.
1. Jika A=0 dan B=0 dijumlahkan, hasilnya S (Sum) = 0.
2. Jika A=0 dan B=1 dijumlahkan, hasilnya S (Sum) = 1.
3. Jika A=1 dan B=0 dijumlahkan, hasilnya S (Sum) = 1.
4. Jika A=1 dan B=1 dijumlahkan, hasilnya S (Sum) = 0. Dengan nilai pindahan Cout (Carry Out) = 1.
Dengan demikian, half adder memiliki dua masukan (A dan B), dan dua keluaran (S dan Cout).
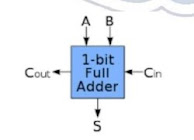
b. Full Adder
Rangkaian Full-Adder, pada prinsipnya bekerja seperti Half-Adder, tetapi mampu menampung bilangan Carry dari hasil penjumlahan sebelumnya. Jadi jumlah inputnya ada 3 : A, B dan Cin, sementara bagian outputnya ada 2: Sum dan Cout. Cin ini dipakai untuk menampung bit Carry dari penjumlahan sebelumnya.
Berikut merupakan symbol dari Full Adder
Rangkaian Full Adder dapat dibuat dengan menggabung 2 buah Half Adder. Rangkaian ini dapat digunakan untuk penjumlahan sampai 1 bit. Jika ingin menjumlahkan lebih dari 1 bit, dapat menggunakan rangkaian Paralel Adder yaitu gabungan dari beberapa Full Adder.
2. Subtractor
Merupakan Suatu Rangkaian Pengurangan 2 buah bilangan biner. Jenis-jenis rangkaian Subtractor yaitu :
a. Half Subtractor
Rangkaian half subtractor adalah rangkaian Subtractor yang paling sederhana. Pada dasarnta rangkaian half subtractor adalah rangkaian half adder yang dimodifikasi dengan menambahkan gerbang NOT. Rangkaian half subtractor dapat dibuat dari sebuah gerbang AND, Gerang X-OR, dan gerbang NOT.
Rangkaian ini mempunyai dua input dan dua output yaitu Sum dan Borrow Out (Bo). Rumus dasar pengurangan pada biner yaitu :
1. 0 – 0 = 0 Borrow 0
2. 0 – 1 = 1 Borrow 1
3. 1 – 0 = 1 Borrow 0
4. 1 – 1 = 0 Borrow 0
b. Full Subtractor
Pada Rangkaian full subtractor pin Borrow Out dihubungkan dengan pin Borrow In(Bin) sebelumnya dan pin Bin di hubungkan dengan pin Bout pada rangkaian berikutnya begitu seterusnya. Sehingga pada rangkaian Full Subtractor mempunyai 3 input dan 2 output.
Berikut merupakan symbol dari Full Subtractor
Rangkaian ini dapat digunakan untuk penjumlahan sampai 1 bit. Jika ingin menjumlahkan lebih dari 1 bit, dapat menggunakan rangkaian Paralel Subtractor yaitu gabungan dari beberapa Full Subtractor.
POKOK BAHASAN V
ENKODER DAN DEKODER
TUJUAN
Setelah menyelesaikan percobaan ini Mahasiswa diharapkan mampu :
- Mengenal rangkaian encoder dan decoder.
- Mengenal rangkaian encoder dan decoder dalam bentuk IC.
PEMBAHASAN
1. ENKODER
a. Rangkailah gerbang logika encoder 4 – 2 berikut ini :
b. Sambungkan terminal input dengan Interactive Input dan terminal output dengan LED.
c. Jalankan program.
d. Amati dan catat output terhadap kombinasi keadaan input.
2. DEKODER
a. Rangkailah gerbang logika decoder 2 – 4 berikut ini :
b. Sambungkan terminal input dengan Interactive Input terminal output dengan LED.
c. Jalankan program.
d. Amati dan catat output terhadap kombinasi keadaan input.
POKOK BAHASAN VI
MULTIPLEKSER DAN DEMULTIPLEKSER
TUJUAN
Setelah menyelesaikan percobaan ini Mahasiswa diharapkan mampu :
- Mengenal rangkaian enkoder dan dekoder.
- Mengenal rangkaian enkoder dan dekoder dalam bentuk IC.
PEMBAHASAN
1. MULTIPLEKSER
a. Rangkaian gerbang logika Multiplekser 4 – 1 berikut ini :
b. Sambungkan terminal input dengan Interactive Input dan terminal output dengan LED.
c. Jalankan program.
d. Amati dan catat output terhadap kombinasi keadaan input.
2. DEMULTIPLEKSER
a. Rangkaian gerbang logika decoder 1 – 4 berikut ini :
b. Sambungkan terminal input dengan Interactive Input dan terminal output dengan LED.
c. Jalankan program.
d. Amati dan catat output terhadap kombinasi keadaan input.



































Tidak ada komentar:
Posting Komentar